- Byteballの合意形成アルゴリズムについて、ホワイトペーパーを読んだ限りでの自分の理解を記録する。
- ここで合意すべき内容とは、同じユーザーが生成したノード群の順序である。
- 具体的には 合意形成 = f (MC(best parent(witness(個人の価値観)))) という構造である。
—
DAGを採用しているペイメントプロジェクトとして有名なByteball。その合意形成アルゴリズムについては「blockchainに基づかない独特なアルゴリズムで…」あるいは「12人のwitnessで決めてられていて…」などと指摘している記事はよく見かけるものの、詳細な記述が少ないように感じたため、ホワイトペーパーを精読してみました。内容について忘れない内にメモしておきます。
前提:
DAG(有向非循環グラフ)とは:
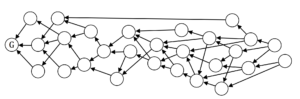
このような構造を持つもの(出典: ホワイトペーパー)で、ノートとエッジから成る。Byteballにおいてはそれぞれ以下を意味する。
| ノード: | 取引記録。送金情報(output)と、その送金の全部または一部となった過去の自身への着金情報(input)の2つで構成されている。(いわゆるUTXO方式) |
| エッジ: | ノードの参照関係。Byteballでは、ノードは既に存在するノードから少なくとも2つをparent nodeとして参照せねばならない。 |
目的:
Byteballにおいて合意すべき内容とは、同じユーザーが作成したノード全てに順序を付けることである。この合意形成によってもし中身が全く同じノードが複数存在する(二重支払い)場合には、順序が前のノードを正しいものとすることで二重支払いを防ぐことが出来る。
*Byteballにおいて、中身が全く同じノードが複数存在するのは整合性が取れない。
この時、もし一方が他方のノードを間接的にでも参照していれば順序は明白だが、以下の図(出典: ホワイトペーパー)のように参照関係が無い場合には順序は不明確である。

手段:
では、参照関係が無い場合どのようにして順序を決めるのか?
まず、DAGの中からメインとなるチェーン(MC)を1本決め、MC上のノードに順序毎に番号を振る。
次に、MCに含まれないノードへは下図(出典: ホワイトペーパー)のように初めて参照されたMC上のノードと同じ番号を振る。これによって、参照関係が無いノードにも番号を付けることが出来る。
*この番号すらも同じになってしまった場合には、ハッシュ値が小さい方のノードを正しいものとする。

では、どのようにしてMCを決めるのか?
新規ノードは、参照しているparent nodeの中から1つbest parentを選択せねばならない。この時parent nodeも自身にとってのbest parentを選択済なので、これを遡ることでいつかは共通のMCへと収束する。
つまり、best parentの選択は各parent nodeに1本ずつ対応するMC候補の中からより望ましいものを選択する行為に等しい。
では、どのようにしてbest parentを決めるのか?
12人のwitnessと呼ばれるユーザーの存在を仮定し、その内の過半数(7人)が作ったノードが全て出現するまで各MC候補を遡る。
それらが全て現れた段階でストップし、その場所にあるノードとgenesisノード(DAGの一番初めのノード)との間の最長経路の距離を測る。
各MC候補間でこの距離を比較し、より長い方をMCに、そしてそれに含まれるparent nodeをbest parentとする。
つまりより直近の取引が過半数のwitnessによるノードに参照されている方を「正しい」MCとしている。
では、どのようにしてwitnessを決めるのか?
12人のwitnessは、各ユーザーが自身の希望をウォレット内のリストに入れることによって選択する。つまりDAG全体で共通の12人を用いる訳では無く、witnessはユーザー毎に異なっている。
従ってbest parentの選択もノード毎に異なったwitnessに基いて行われるが、一方でwitnessリストの内容が2つ以上異なっているユーザーのノードはbest parentに選択出来ないという制限が課されている。
よってMCはwitnessに関して同じような価値観を持ったノードの連なりであり、価値観が変化するペースは緩やかである。
まとめ:
つまり関数のように書くと、
合意形成 = f (MC(best parent(witness(個人の価値観))))
という構造になっている。
—
次回はこの合意形成アルゴリズムに対する疑問点や要議論点について書く予定です。また、内容に誤りがある場合にはご指摘いただければ幸いです。
